LPS aims to close the gap between logical and imperative computer languages, by performing actions to generate models to make goals of the logical form if antecedent then consequent true. Model generation serves as a global imperative, which generates commands to make consequents true whenever antecedents become true.

LPS also includes beliefs of the logical form conclusion if conditions. In addition to their logical interpretation, beliefs also have an imperative interpretation as procedures, which make or determine whether a conclusion is true by making or determining whether the conditions are true.

Arguably, this combination of goals and beliefs not only unifies different computing paradigms, but also serves as a scaled-down model of human thinking. Goals in LPS are a logical reconstruction of condition-action rules in the production system model of human thinking [8]. Beliefs in LPS are logic programs, which have been shown to model human reasoning in psychological studies such as [7] and in normative studies such as [6]. They have also been used to teach computational thinking [5].

There are now two online, open-source prototypes of LPS. The first, implemented in SWI Prolog and running on SWISH [9], was developed as part of the project CLOUT (Computational Logic for Use in Teaching), funded by Imperial College London, to support the teaching of computing and logic in schools. The prototype has been  extended by the startup Logical Contracts to facilitate the representation and execution legal contracts. In applications to logical contracts, beliefs support the representation of constitutive rules, which define legal concepts, and goals support the representation of regulatory rules, which express obligations and prohibitions.

To try LPS on SWISH, click here, go to the Examples menu, and click on LPS Examples, First steps with LPS or Fintech examples.

For example, here is a screenshot of an LPS SWISH program with two reactive rules, which transfer funds between Bob and Fariba:

To run the example, type go(T) into the SWISH query box. You will get a Gantt chart showing the timeline of facts updated by observations of external events and by actions performed by the system. For example:

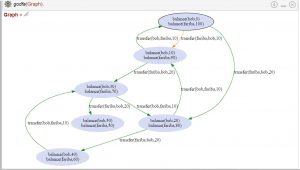
If you type godfa(Graph) instead, you will get a more abstract visualisation of states and state transitions:

There is also an experimental Prolog programmable 2D animation:

The open source of the extended prototype is available at the LPS bitbucket site.

The second prototype, lps.js, written in JavaScript, was implemented by Sam Yong as an MSc project at Imperial College London. It can be used to run LPS programs in web browsers and the Node.js runtime. The “Getting Started” usage guide can be found on https://lps.js.org/. To try the sandbox, click here.

lps.js has been extended to build a desktop application, LPS Studio, to visualise LPS programs for interactive storytelling using the Electron framework.

There is also a much simpler LPS game for teaching logic and computing to children. You can download the game from here.

For more information about LPS, go to the LPS bitbucket site or see [1,2,3,4].

References.

1. Kowalski, R. and Sadri, F. (2015) Reactive Computing as Model Generation.
New Generation Computing, 33, 1, 33-67.

2. Kowalski, R. and Sadri, F. (2016) Programming in Logic without Logic Programming.
TPLP, 16, 269-295.

3. Kowalski, R. and Sadri, F. (2016) Introduction to LPS.

4. Kowalski, R. (2011) Computational Logic and Human Thinking – How to be Artificially Intelligent.
Cambridge University Press.

5. Levesque, H. J. (2012). Thinking as Computation: A First Course. MIT Press.

6. Pereira, L. M., & Saptawijaya, A. (2016). Programming Machine Ethics (Vol. 26). Springer.

7. Stenning, K., & Van Lambalgen, M. (2012). Human reasoning and cognitive science. MIT Press.

8. Thagard, P. (1996). Mind: Introduction to cognitive science (Vol. 4). Cambridge, MA: MIT press.

9. Jan Wielemaker, Fabrizio Riguzzi, Robert Kowalski, Torbjorn Lager, Fariba Sadri, Miguel Calejo. (2019). Using SWISH to realise interactive web based tutorials for logic based languages  Theory and Practice of Logic Programming, 19(2), 229-261.